Математический сопроцессор: основные функции

Один из наиболее распространенных типов сопроцессоров - математический сопроцессор. Математический сопроцессор предназначен для быстрого выполнения арифметических операций с плавающей точкой, предоставления часто используемых вещественных констант (

, log210, log2e, ln2, :), вычисления тригонометрических и прочих трансцендентных функций (tg, arctg, log, ...).

Большинство современных математических сопроцессоров для представления вещественных чисел используют стандарт IEEE 754-1985 "IEEE1) Standard for Binary Floating-Point Arithmetics". Старший разряд двоичного представления вещественного числа всегда кодирует знак числа. Остальная часть разбивается на две части: экспоненту и мантиссу. Вещественное число вычисляется как: (-1)S·2E·M, где S - знаковый бит числа, E - экспонента, M - мантисса. Если 1

M<2, то такое число называется нормализованным. При хранении нормализованных чисел сопроцессор отбрасывает целую часть мантиссы (она всегда 1), сохраняя лишь дробную часть. Экспонента кодируется со сдвигом на половину разрядной сетки, таким образом, удается избежать вопроса о кодировании знака экспоненты. Т.е. при 8-битной разрядности экспоненты код 0 соответствует числу -127, 1 - числу -126, ..., 255 числу +126 (экспонента вычисляется как код 127).

Стандарт IEEE-754 определяет три основных способа кодирования (типа) вещественных чисел.

Таблица 8.1. Типы (способы кодирования) вещественных чисел

ТипДиапазон значений(по модулю)Двоичное представление

вещественное ординарной точности (single precision) - 32 бит

1,18·10-38... 3,40·1038

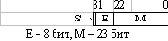вещественное двойной точности (double precision) - 64 бит

2,23·10-308... 1,79·10308

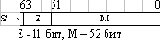вещественное расширенной точности (extended precision) - 80 бит

3,37·10-4932... 1,18·104392

Приведем пример кодирования вещественного числа 178,625:

178,62510 = 128 + 32 + 16 + 2 + 0,5 + 0,125 = = 1·27 + 0·26 + 1·25 + 1·24 + + 0·23 + 0·22 + 1·21 + 0·20 + + 1·2-1 + 0·2-2 + 1·2-3 = 10110010,1012

Для представления этого числа в соответствии с IEEE-754 его нужно нормализовать (привести в экспоненциальный вид):

Содержание раздела